Expand (x2)^3 (x 2)3 ( x 2) 3 Use the Binomial Theorem x3 3x2 ⋅23x⋅ 22 23 x 3 3 x 2 ⋅ 2 3 x ⋅ 2 2 2 3 Simplify each term Tap for more steps Multiply 2 2 by 3 3 x 3 6 x 2 3 x ⋅ 2 2 2 3 x 3 6 x 2 3 x ⋅ 2 2 2 3 Raise 2 2 to the power of 2 2You can Expand \( (x2)^3 \) through formulas and simple multiplication method I am going to expand \( (x2)^3 \) through the formulaHow do you expand ( 2 x − y ) 5 using Pascal's Triangle?
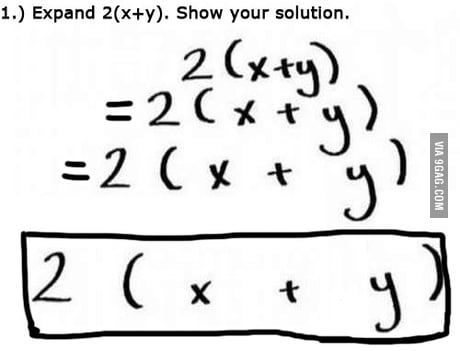
Expand 2 X Y 9gag
Expand the binomial (x^2-y^2)^3
Expand the binomial (x^2-y^2)^3- How do you expand the binomial #(x2)^3#?Consider the right hand side (R H S) and expand it as follows (x (1 2 x 2 1 0 3 x y 2 5 y 2) Medium View solution View more Learn with content Watch learning videos, swipe through stories, and browse through concepts Concepts > Videos



1
The following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) Cube How do you find the coefficient of x^5 in the expansion of (2x3)(x1)^8?" Let's solve the problem The expression is = (2x y)^3 The expression is equal to (2x y)^2 (2x y) Then it is equal to (4x^2 4xy y^2) (2x y) Then it is equal to 8x^3 4x^2y 8x^2y 4xy^2 2xy^2 y^3 Then it is equal to 8x^3 12x^
So (x − 2 y) 3 = x 3 − 3 (x) 2 (2 y) 3 x (2 y) 2 − (2 y) 3 = How do you expand \displaystyle{\left({2}{x}{y}\right)}^{{5}} using Pascal's Triangle?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Precalculus The Binomial Theorem Pascal's Triangle and Binomial Expansion 1 Answer
Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Expand Evaluate Fractions Linear Equations Quadratic Equations Inequalities Systems of Equations Matrices Substitute 2 for y in x=\frac{2}{3}y\frac{22}{3} Because the resulting equation contains only one variable, you can solve for x directlyBinomial Theorem Formula Use the formula for the binomial theorem to determine the fourth term in the expansion (y − 1) 7 Show Answer Problem 2 Make use of the binomial theorem formula to determine the eleventh term in the expansion (2a − 2) 12




Section 9 Binomial Expansion Questions About Homework Submit Homework Recall The Exercises We Did Last Class 04 01 19 Math 106 Section 9 1 Slideshow And Powerpoint Viewer What Is Binomi




Alg2 March28 The Answers
Thus the given expression is identically equal to 2 y ( 2 x x 2 − y 2) x y x − y In the case where x greatly exceeds y, the numerator is essentially 2 y ( 3 x) = 6 x y, and the denominator is approximately 2 x Therefore, the given expression is roughly 3 x 1 / 2 y, as claimedExpandcalculator Expand (x^23y)^3 en Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the next few weeks, we'll be showing how Symbolab taking the square root of both sides we get LATEXR=\pm (x^2y^2)^\frac {1} {2} /LATEX and taking that up to the third power we get LATEXR^3=\pm (x^2y^2)^\frac {3} {2} /LATEX so that whole right side is equal to LATEXR^3 /LATEX Last edited
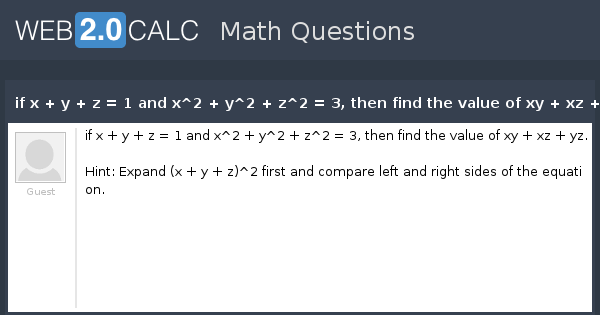



View Question If X Y Z 1 And X 2 Y 2 Z 2 3 Then Find The Value Of Xy Xz Yz




Binomial Expansion Christober S Technical Weblog
How do you use the binomial series to expand #f(x)=1/(sqrt(1x^2))#?The Binomial Theorem is a formula that can be used to expand any binomial (xy)n =∑n k=0(n k)xn−kyk =xn(n 1)xn−1y(n 2)xn−2y2( n n−1)xyn−1yn ( x y) n = ∑ k = 0 n ( n k) x n − k y k = x n ( n 1) x n − 1 y ( n 2) x n − 2 y 2 ( n n − 1) x y n − 1 y nBinomial Expansions Binomial Expansions Notice that (x y) 0 = 1 (x y) 2 = x 2 2xy y 2 (x y) 3 = x 3 3x 3 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 Notice that the powers are descending in x and ascending in yAlthough FOILing is one way to solve these problems, there is a much easier way




Find The Coefficient Of X 6y 3in The Expansion Of X 2y 9



Use The Binomial Theorem To Expand And Simplify Each Expression X Y 8 What Is The Answer Quora
I found the maximum(√3) an minimum(√3/2) values using logic and a sketch of the trigonometric circle I want to know a way to find the answer using more math instead of the way I did, because maybe it was only luck to find it(x y) 3 = x 3 3x 2 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4;The calculator allows you to expand and collapse an expression online , to achieve this, the calculator combines the functions collapse and expand For example it is possible to expand and reduce the expression following ( 3 x 1) ( 2 x 4), The calculator will returns the expression in two forms expanded and reduced expression 4 14 ⋅ x




Question 1 1 What Is The Coefficient Of Roy2 In The Chegg Com




Using Suitable Identities Expand The Following I Left Dfrac X 5 3y Right 2 Ii Left 11x 0 2y Right 2 Iii Left 4a 5b Right 2 Iv Left Y
Show, by left side, that $$\frac{x^3y^3}{xy} = x^2xyy^2,$$ or $$\frac{x^3y^3}{x^2xyy^2} = xy$$ You may read about "Long Division of Polynomials" See3x^ {2}6x12y^ {2}3 3x2 − 6x − 12y 2 3 View solution steps Solution Steps ( 3 ) ( x 2 y 1 ) ( x 2 y 1 ) ( 3) ( x 2 y − 1) ( x − 2 y − 1) Use the distributive property to multiply 3 by x2y1 Use the distributive property to multiply 3 by x 2 y − 1 \left (3x6y3\right)\left (x2y1\right)Expand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3




Expanding Binomials Video Polynomials Khan Academy



22 X 1 3 Expand Pictures
Solve for x Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0 So the expansion becomes (x2y)^7 = 1x^7y^07x^6(2y)^121x^5(2y)^235x^4(2y)^335x^3(2y)^421x^2(2y)^57x^1(2y)^61x^0(2y)^7 Cleaned up a bit, it becomes (x2y)^7 = x^714x^6y84x^5y^2280x^4y^3560x^3y^4672x^2y^5448x^1y^6128y^7 In this finalAn outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for their




Ex 8 2 5 Find 4th Term Of X 2y 12 Chapter 8 Class 11




3 Expand With The Help Of Formula X Y 3 2
Learn how to expand and simplify (x2)(x3) using FOIL MethodThe FOIL method is a process used to multiply two binomials and remove the bracketsMusic by Adr⋅(x)3−k ⋅(−y)k ∑ k = 0 3 #(xy)^6=x^66x^5y15x^4y^2x^3y^315x^2y^46xy^5y^6# Explanation The Binomial Theorem gives a time efficient way to expand




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf




Expand And Simplify I 3 X Y 24 Ii P 2 Q3 Gauthmath
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial According to the theorem, it is possible to expand the polynomial n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive integer depending on n and b For example, 4 = x 4 4 x 3 y 6 x 2 y 2 4 x y 3 y 4 {\displaystyle ^{4}=x^{4}4x^{3}y6x^{2}y^{2}4xy^{3}y Find an answer to your question expand (x÷2y÷3)square asitpatro asitpatro Math Secondary School Expand (x÷2y÷3)square 2 See answers SyedNomanShah SyedNomanShah Answer Hope its helpful for youHow do you find the coefficient of x^6 in the expansion of #(2x3)^10#?




Obtainthe Taylor S Seriesexpansion Of X3 Y3 Xy 2 Interms Of Powers Of X 1 And Y 2 Up To Third Brainly In



What Is The Binomial Expansion Of Math 1 X 2 Math Quora
Learn about expand using our free math solver with stepbystep solutions Microsoft Math Solver Solve Practice Download Solve Practice Topics (x3)(x2)(x1) (x\log _2(x1)=\log _3(27) 3^x=9^{x5} equationcalculator expand (y3)(y1) en Related Symbolab blog posts High School Math Solutions – Quadratic Equations Calculator, Part 1−2x (x − y − z) = −2×2 2xy 2xz Example 3 Expand −3a 2 (3 − b) Solution Apply the distributive property to multiply −3a 2 by all terms within the parenthesis
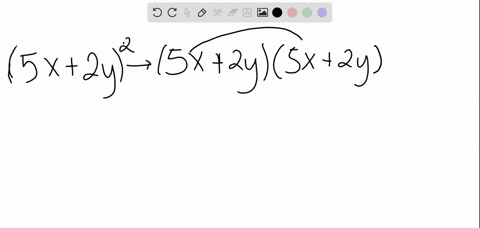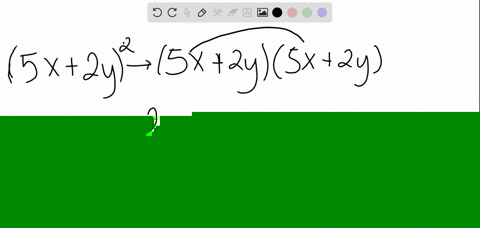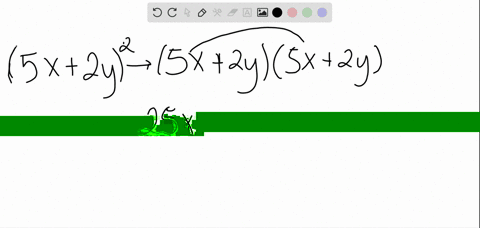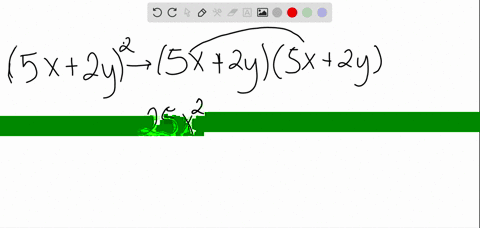



Solved Expand X Y 5
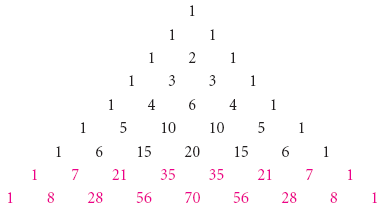



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
Expand (xy)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Multiply by Add andExpand (− 2 x 5 y − 3 z) 2 using suitable identities Hard Answer (− 2 x 5 y − 3 z) 2 is of the form (a b c) 2 (a b c) 2 = a 2 b 2 c 2 2 a b 2 b c 2 c a where a = − 2 x, b = 5 y, c = − 3 z ∴ (− 2 x 5 y − 3 z) 2 =Start your free trial In partnership with You are being redirected to Course Hero I want to submit the same problem to Course Hero Cancel




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9



Plos Computational Biology Post Lockdown Abatement Of Covid 19 By Fast Periodic Switching
y = x − x 2 and the result is (2) ( 2 x − x 2) 2 = 64 192 ( x − x 2) 240 ( x − x 2) 2 160 ( x − x 2) 3 ⋯ Since we only need an expansion with powers up to x 3 we don't need any terms ( x − x 2) n with n > 3 We also recall the binomial formulas ( a b) n for n = 2, 3The second term of the sum is equal to Y The second factor of the product is equal to a sum consisting of 2 terms The first term of the sum is equal to X The second term of the sum is equal to negative Y open bracket X plus Y close bracket multiplied by open parenthesis X plus negative Y close parenthesis;👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms or




Expand 1x Y3 3 Maths Questions



Http Walkinginmathland Weebly Com Uploads 6 7 8 8 Binomial Expansion Worksheet Pdf
Find the product of two binomials Use the distributive property to multiply any two polynomials In the previous section you learned that the product A (2x y) expands to A (2x) A (y) Now consider the product (3x z) (2x y) Since (3x z) is in parentheses, we can treat it as a single factor and expand (3x z) (2x y) in the sameExpand ( X 2y 2 )2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 5 Question Bank Solutions Concept Notes & Videos 258 Syllabus Advertisement Remove all ads Expand ( X 2y 2 )2 MathematicsExample 2 Expand −2x (x − y − z) Solution Multiply −2x by all terms inside the parenthesis and change the operators accordingly;




Assessment Algebra Dev Assessment In Algebra Lb Hour If And Evaluate The Following Expressions Simplify 10 Expand Xy Axz Simplify 12 15 Ab Simplify 10 Solve Studocu



What Is The Binomial Expansion For 1 X 1 Quora
This calculator can be used to expand and simplify any polynomial expressionAlgebra Expand using the Binomial Theorem (xy)^3 (x − y)3 ( x y) 3 Use the binomial expansion theorem to find each term The binomial theorem states (ab)n = n ∑ k=0nCk⋅(an−kbk) ( a b) n = ∑ k = 0 n n C k ⋅ ( a n k b k) 3 ∑ k=0 3!Expand (x^22x2) (x^212x37) \square!




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9



8 4 Pascals Triangle And The Binomial Theorem
${5 \choose 2} 3x^4y^3 = 10 \times 3x^4y^3 = 30x^4y^3$ My answer was way off My powers were all correct but my coefficients were way off, not even in the same ballparkAlgebra Expand using the Binomial Theorem (xy)^2 (x − y)2 ( x y) 2 Use the binomial expansion theorem to find each term The binomial theorem states (ab)n = n ∑ k=0nCk⋅(an−kbk) ( a b) n = ∑ k = 0 n n C k ⋅ ( a n k b k) 2 ∑ k=0 2! Expand (1/xy/3)^3 solve it fastly राम, बॉबी और सलमान तीन आदमियों की आयु का योग 154 वर्ष है। यदि राम की आयु, बॉबी की आयु की दुगुनी तथा सलमान की आयु की तिगुनी है, तो सलमान की आयु



Alg2 10 5 Part 2 Binomial Expansion Mrsb Schooltube Safe Video Sharing And Management For K12




Expanding Brackets Expand 2 Single And Simplify Teaching Resources
How Do You Expand \( (x2)^3 \)?The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3⋅(x)2−k ⋅(−y)k ∑ k = 0 2




Themathbooklets S2 N5 Expansion Of 2 Linear Expressions Add And Subtract Of Quadratic Expressions




Expand Calcme Documentation Wiris




X Y 2 3 Find The Expansion Of The Following Brainly In




Find These Asymptotes Of Thes See How To Solve It At Qanda
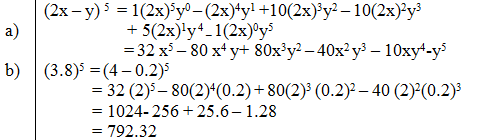



A Expand And Simplify The Binomial Expression 2x Y Sup 5 Sup B Use The First Four Terms Of The Expansion Above To Approximate The Value Of 3 8 Sup 5 Sup




Ppt The Binomial Theorem Powerpoint Presentation Free Download Id



Expand X Y 3 Sarthaks Econnect Largest Online Education Community



Basic Log Rules Expanding Log Expressions Purplemath




Expand The Given Expression 3 X3 X Y 4 Z 33 X Gauthmath




Pls Solve It Fast 5 6 8 9 14 15 Expand Use Appropriate Formulae Maths Meritnation Com



Www Nuffieldfoundation Org Sites Default Files Files Fsmq algebraic expressions Pdf




Expand And Simplify I 3 X Y 24 Ii P 2 Q3 Gauthmath



2
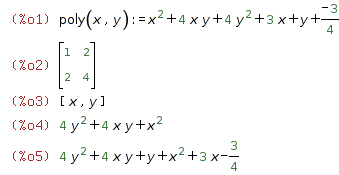



Wxmaxima Html Export




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange




Expanding Brackets Key Stage 3




Pdf High Temperature Expansion Of The Free Energy In The Two Dimensional Xy Model




Limit Calculator Wolfram Alpha



Http Kinetonmathsdepartment Weebly Com Uploads 5 5 2 7 Expanding Factorisinghw2 Pdf




Algebra Expansion And Factorisation Pdf Free Download




Expand X Y 3 And X Y 2 Brainly In




Expand 2x Y 2 2 Novocom Top



Q Tbn And9gcsc77taatmdq7zu7mkjpjo14wu24cor9x8c Pdyonmo Vpvzmuz Usqp Cau



Expansion And Factorisation Bingo Card




Binomial



1
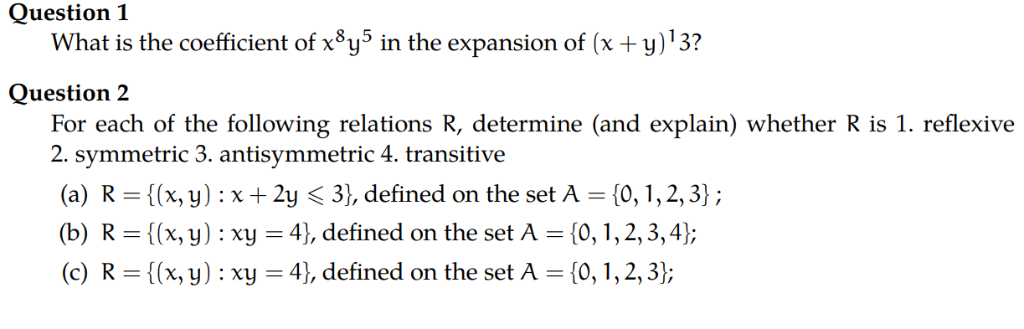



Question 1 What Is The Coefficient Of X8y5 In The Chegg Com




Using The Binomial Theorem College Algebra
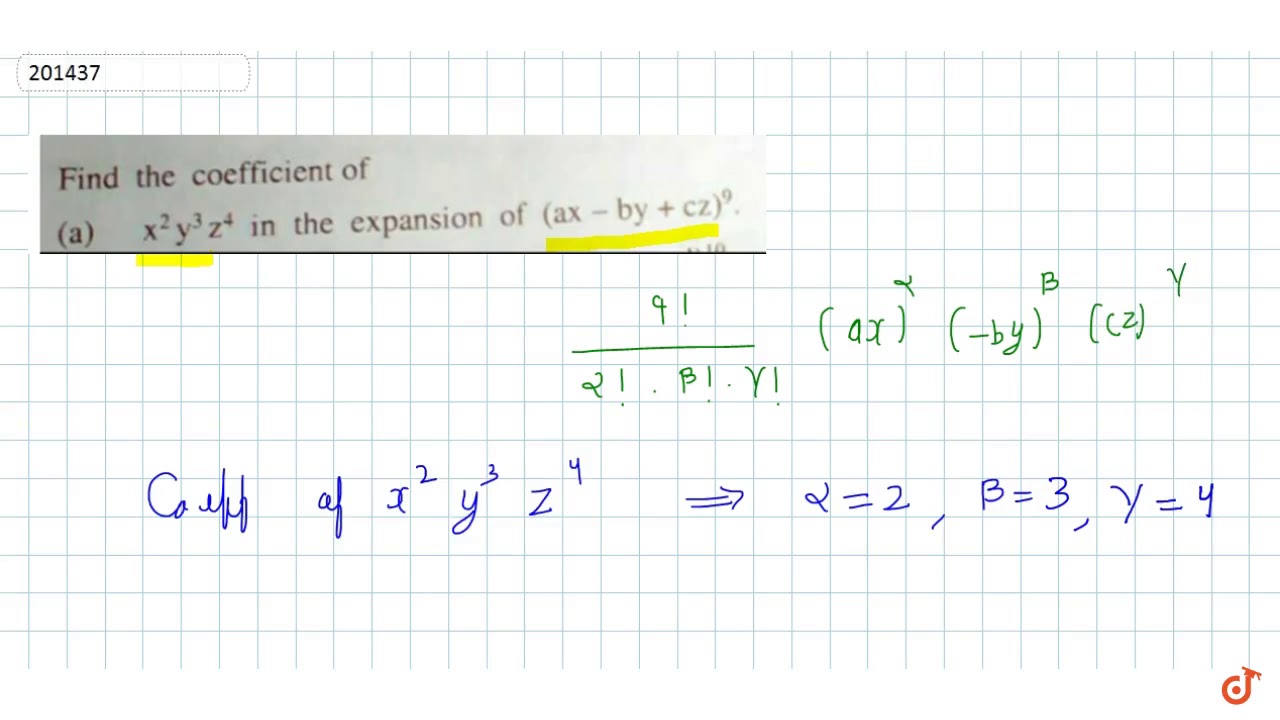



Find The Coefficient Of X 2 Y 3 Z 4 In The Expansion Of Ax By Cz 9 Youtube




Partial Fraction Expansion Video Khan Academy



Expand 2 X Y 9gag




Extrema Taylor S Expansion Maxima And Minima Mathematical Concepts




Taylor Series Expand X 2y 3y 2 In The Powers Of X 1 And Y 2 Up To 3 Degree Terms Youtube



2fv5d843v9w22sxtto1ibxtu Wpengine Netdna Ssl Com Wp Content Uploads 13 06 June 13 1ma0 1h Q4 Expand Brackets Pdf



What Is The Binomial Expansion For 1 X 1 Quora



4 The Binomial Theorem




X 2 3 Expand Novocom Top




Binomial Theorem Wikipedia




9 5 The Binomial Theorem




Expand 2 X Minus 3 Y 4 Z Whole Square Maths Linear Equations In One Variable Meritnation Com




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube
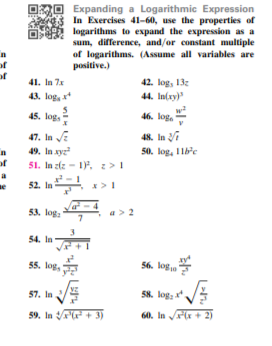



Answered O Expanding A Logarithmic Expression In Bartleby




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




A Quick And Efficient Way To Expand Binomials Ppt Download




Algebra Expansion And Factorisation Pdf Free Download




Expand 2x Y 5 With The Help Of Binomial Theorem



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver
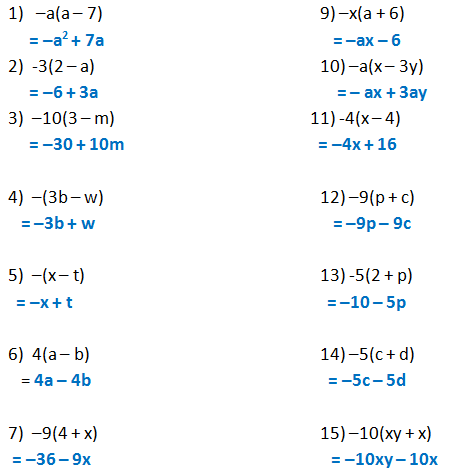



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths




Binomial Theorem



Find The Coefficient Of The Term X 6y 3 In The Expansion Of X 2y 9 Sarthaks Econnect Largest Online Education Community
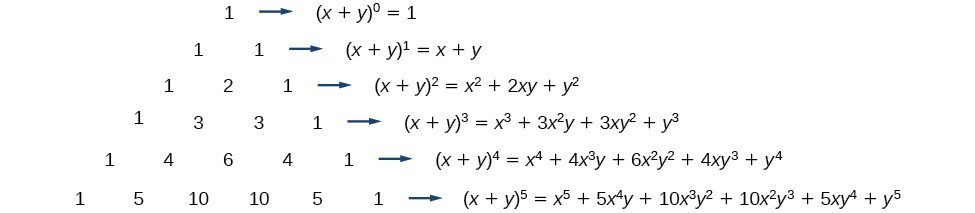



Using The Binomial Theorem College Algebra



How To Expand 2x Y 3 Quora




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



2 Expand And Simplify X 2 X 3 A B 3x 1 2 Chegg Com




Binomial Expansion Made Easy Expand X Y Algebra Youtube




Myriorama Cards Were Invented In France Around 13




Ex 8 2 5 Find 4th Term Of X 2y 12 Chapter 8 Class 11
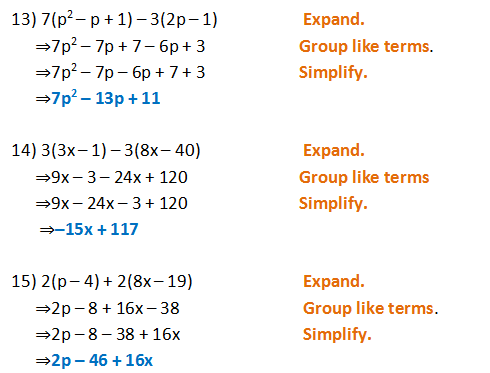



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths
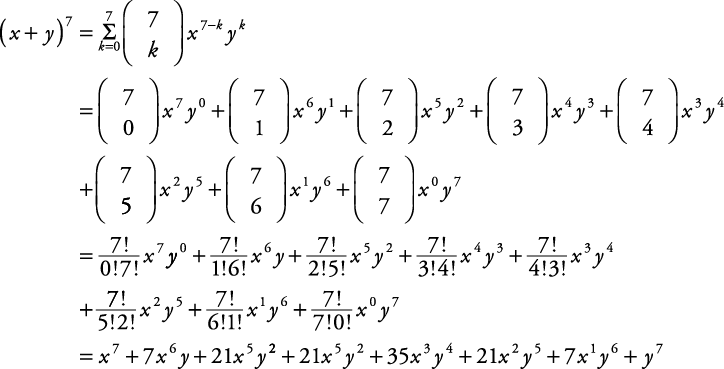



Binomial Coefficients And The Binomial Theorem




Extra Practice




Digital Lesson The Binomial Theorem The Binomial Theorem



1




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




X Y 2 3 Find The Expansion Of The Following Brainly In




Y 1 2x Y 0 Xy 2 X Y 0 A Solve The Chegg Com




X 3y 3 Expand Novocom Top
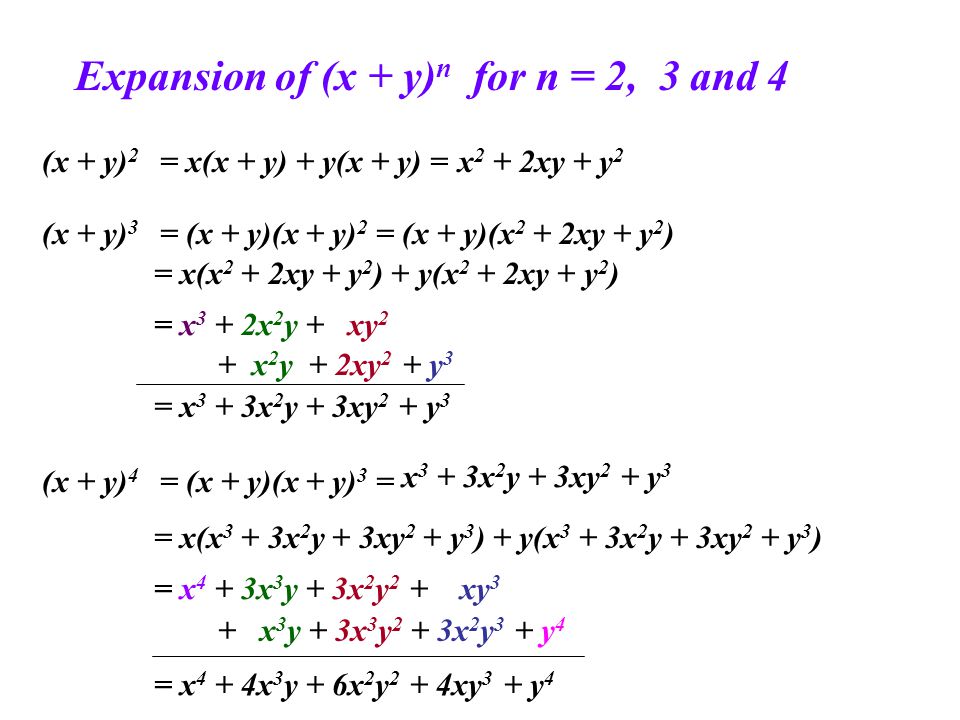



The Binomial Theorem 1 Objectives Pascal S Triangle Coefficient Of X Y N When N Is Large Notation Ncrncr Ppt Download




The Binomial Theorem Notes Answers Binomial Theorem Notes Ans3 3 Using Above Expansion X X Y X Y Xy Y X X Y X Y Xy X Y X Y Xy Y The Binomial Theorem Notes Answers Date Rhhs Pdf Document




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Binomial Theorem By Calum Blair Issuu
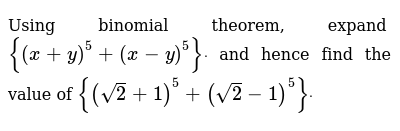



Using Binomial Theorem Expand X Y 5 X Y 5 Dot And Hence Fi



1




Expand And Simplify Binomial Squares 2x 3y 2 Youtube
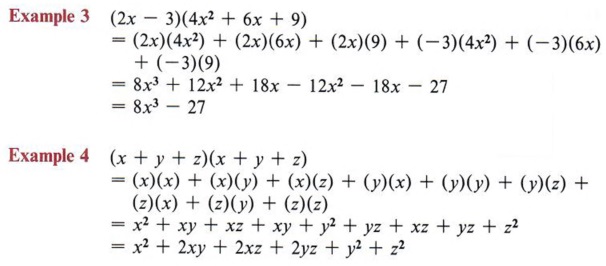



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver




1 1 Expand And Simplify The Following 1 1 1 7x2 Gauthmath



0 件のコメント:
コメントを投稿